Programming Challenges - Week 5 - Review Competition Problems and Intro to Data Structure

Review problems

Homework (Hackeerank)

one way to solve circular array

Practice blogging

Create a new blog
Review Markdown
Add image

Data Structure and Algorithms

Big O Notation

The Big O (pronounced ‘Oh’) notation is used to classify algorithms according to how its running time or space requirements grow as the input size grows (very big, like millions and billions).

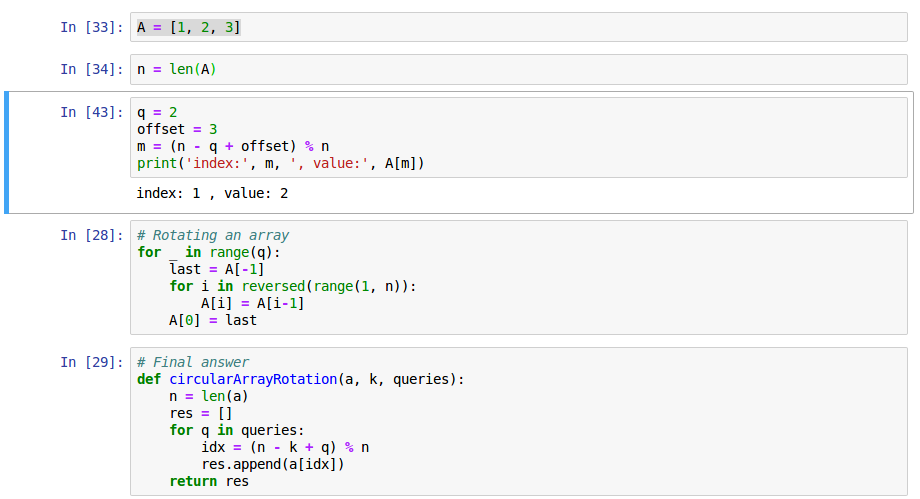
Let’s try a Jupyter notebook. Here are key operations:

Press Shift + Enter to execute a cell.

Loading a matplot libary

Add the following code in the Jupyter notebook, and press Shift + Enter.

%matplotlib inline
import math
import matplotlib.pyplot as plt

Add the following code on the second cell and press Shift + Enter.

N = 1000000 # 1 million

Add the rest of the code and the third cell and press Shift + Enter.

a = [i for i in range(1, N)]  # O(N)
b = [i*i for i in range(N)] # O(N^2)
c = [math.log(i) for i in range(100, N)] # O(log(N))
d = [i * math.log(i) for i in range(100, N)] # O(N*log(N))
plt.ylabel('Time')
plt.xlabel('Size of input')
plot_a, = plt.plot(a, color='blue', label='O(N)')
plot_b, = plt.plot(b, color='red', label='O(N^2)')
plot_c, = plt.plot(c, color='purple', label='O(log(N))')
plot_d, = plt.plot(d, color='green',  label='O(N*log(N))')
plt.legend(handles=[plot_a, plot_b, plot_c, plot_d], loc=1)
plt.show()

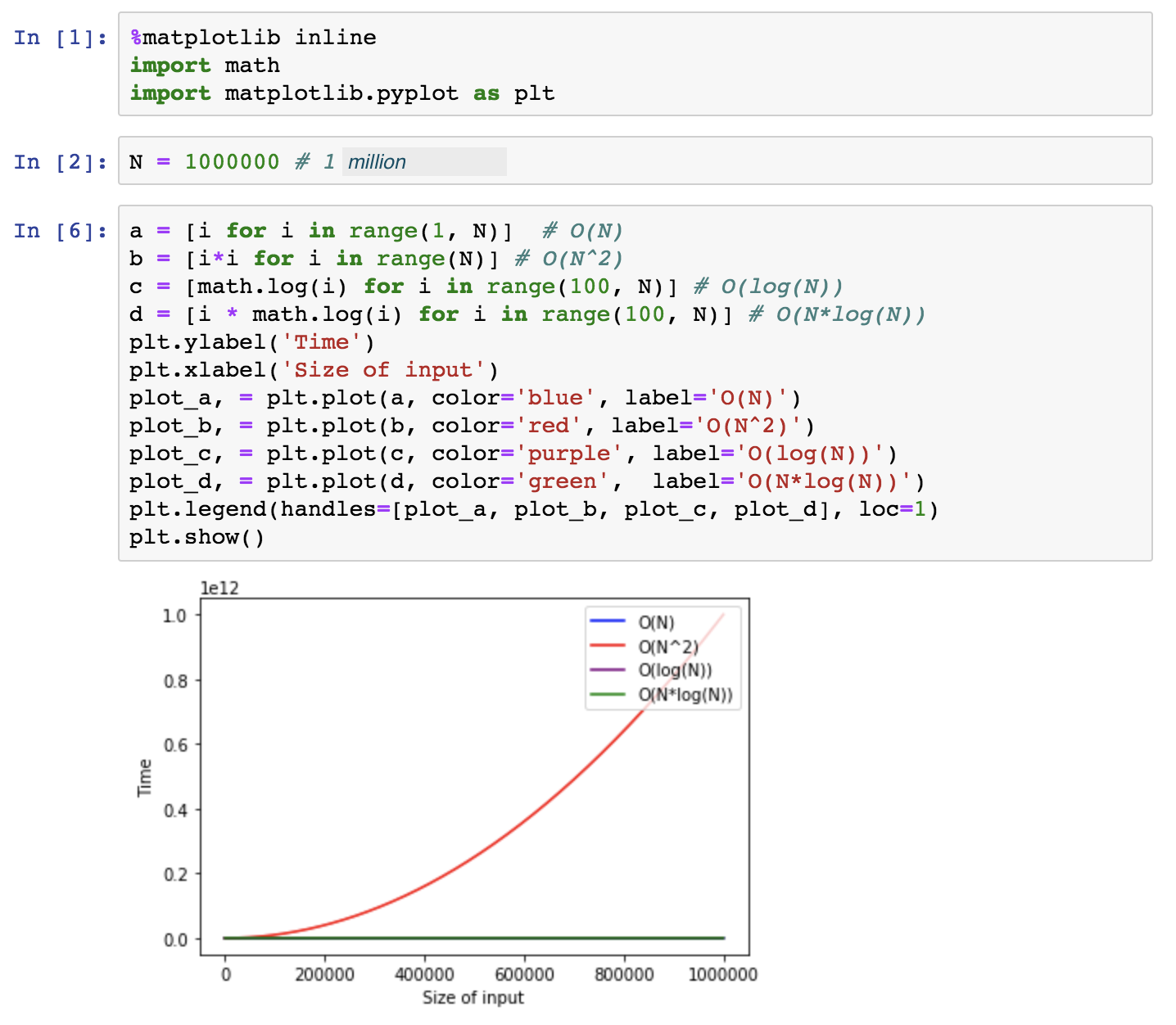
Here are the results. The higher the time (y-axis), the slower the runtime is.

Big O

Data Structure

Primitive Types
Array
Linked List
Hash Table (Dictionary)
Stack and Queue
Tree
Heap
Graph

Array vs. Linked List, Trees and Graphs

Data Structure: Linked List

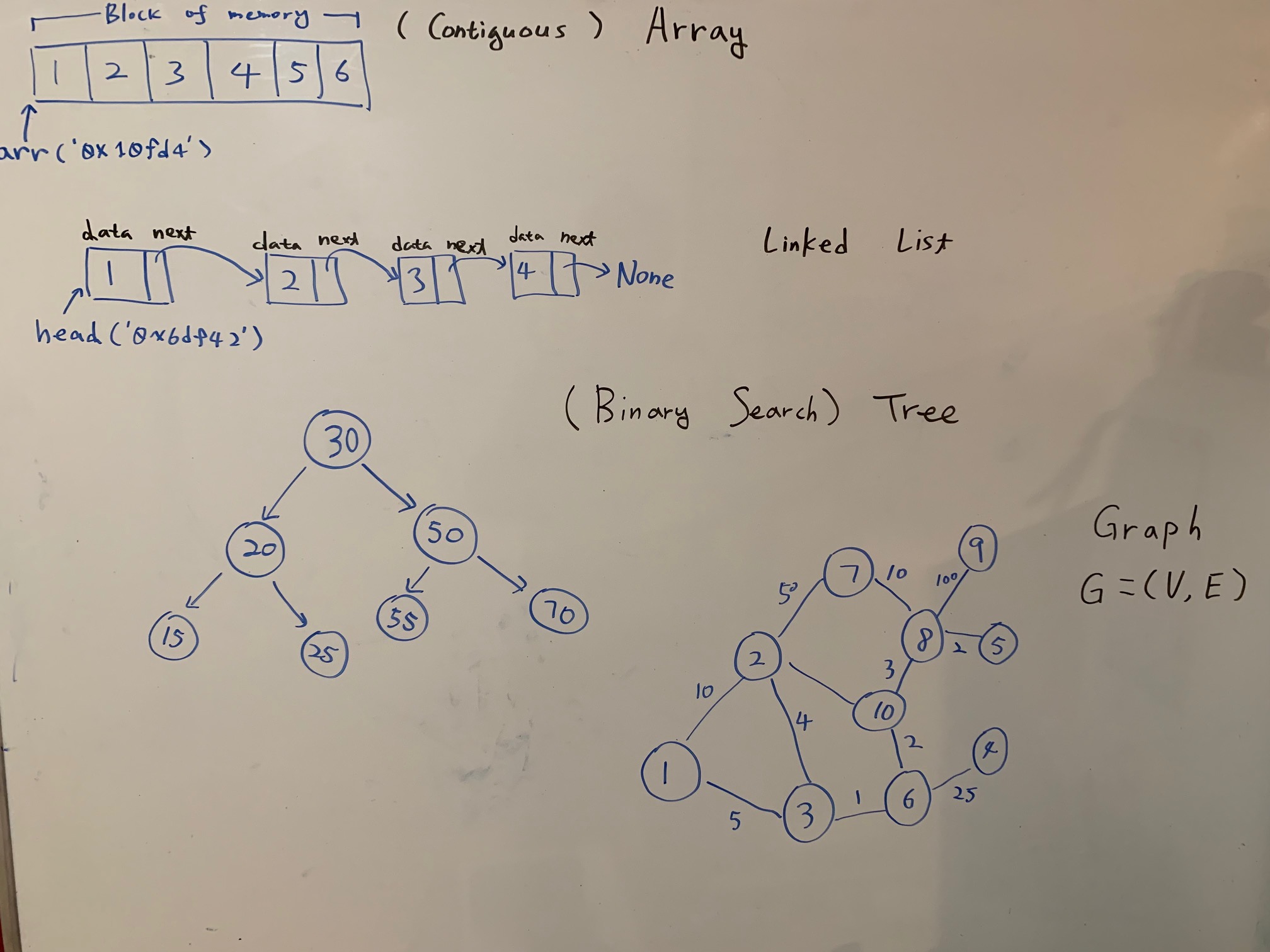
Contiguous vs. Linked Data Structures

Contiguously allocated structures: arrays, heaps, and hash tables
Linked data structures: lists, trees, and graph adjacency lists

class Node:
    """
    Node for Linked List
    """
    def __init__(self, data: int):
        self.data = data
        self.next = None
        
head = Node(1)
assert head.data == 1

Linked List: Insert

def insert(node, data: int):
    """
    Insertion at the beginning to avoid
    traversing the list
    """
    tmp = Node(data)
    tmp.next = node
    node = tmp
    return node

head = Node(1)
assert head.data == 1

head = insert(head, 2)
assert head.data == 2
assert head.next.data == 1    

Linked List: Find

There are two ways to implement the find method – recursively or iteratively. In either case, it takes O(N) time to find an item in a linked list.

# Recursive find
def find_recursive(node, data):
    """
    Recursively traverse the list and
    return a node when its data mathes a provided data
    """
    if node is None:
        return
    if node.data == data:
        return node
    return find_recursive(node.next, data)

def find(head, data):
    """
    Find a node iteratively for a provided data
    """
    tmp = head
    while tmp:
        if tmp.data == data:
            break
        tmp = tmp.next
    return tmp

head = Node(1)
assert head.data == 1

head = insert(head, 2)
assert head.data == 2
assert head.next.data == 1

head = insert(head, 3)
print_list(head)

assert find(head, 7) == None
assert find(head, 3) == head
assert find(head, 2) == head.next    

Linked List: Delete

Deletion is more complicated than other operations. First, we need to find a pointer to the predecessor of the item to be deleted.

def find_predecessor(node, data):
    """
    Find a predecessor of a node of which data matches a provided data
    """
    if node is None or node.next is None:
        return
    if node.next.data == data:
        return node
    else:
        return find_predecessor(node.next, data)

We needed the predecessor so that its next pointer must be changed.

def delete(head, data):
    """
    Deleting a node requires a pointer to a predecessor
    """
    cur = find_recursive(head, data)
    if cur:
        pred = find_predecessor(head, data)
        if pred is None:
             head = cur.next
        else:
            pred.next = cur.next
    return head

Linked List: Print all nodes

def print_list(node):
    """
    Recursively traverse the list and
    print data
    """
    if node is None:
        return
    print(node.data, end=' ')
    print_list(node.next)

Putting all together

Here is the code for the above operations of a linked list.

Practice

Write a function return the length of a linked list.
```
def length_of_list(head):
 pass
```
Write a function to determin if a linked list contains a duplicate value
```
def has_duplicate(head):
 pass
```

Summary

We learned the basic concept of Big O notation, and studied the characteristics of different running time using Jupyter Notebook (which is way cool!).

Linked List is a our first step to learn a linked data structure that is different from a contiguous data structure such as an array. The concept and techniques learend in Linked List are the building blocks for other data structure such as lists, trees and graphs.

Written on March 24, 2019